2ª FORMAÇÃO CONTINUADA 05 A 09 DE MAIO 2014

SLIDE 2ª FORMAÇÃO CONTINUADA EXIBIR APRESENTAÇÃO DE SLIDES BAIXAR TUDO

  MATERIAL DE JOGOS

PREFEITURA MUNICIPAL DE CAMPO GRANDE

ESTADO DE MATO GROSSO DO SUL

SECRETARIA MUNICIPAL DE EDUCAÇÃO

SUPERINTENDÊNCIA DE GESTÃO DE POLÍTICAS EDUCACIONAIS

COORDENADORIA DE ENSINO FUNDAMENTAL – 6^o AO 9^o ANO

OFICINA DE JOGOS

Jogo: subindo e escorregando

Número de participantes: até três jogadores.

Objetivos	. Resolver operações de adição e subtração com números inteiros; . Desenvolver o cálculo mental com números inteiros negativos; . Elaborar estratégias para resolver problemas e atingir os objetivos    estipulados, bem como, executar e validar suas ações.
Material	. Tabuleiro do jogo; . Dois dados numerados de 1 a 6, nas cores: verde e branco; . Peões; . Lápis e borracha.

Regras do jogo:

1. Tira-se par ou ímpar para ver quem começa o jogo;

2. Os jogadores posicionam seus peões no zero;

3. Quando chegar sua vez, cada jogador lança os dois dados. O dado verde mostra quantas
     casas ele vai subir e o branco quantas vai escorregar, tudo na mesma jogada;

4. Cada jogador deve efetuar seu registro anotando: primeiro o valor da casa em que está e
     depois o valor de cada dado e a seguir o resultado;

5. Quem chegar até o -10 sai da jogada ou, se o jogo for com apenas dois jogadores, perde o jogo;

6. O jogo termina quando restar apenas um jogador ou quando alguém chegar ao topo.

Explorando o jogo:

Professor, essas são atividades que podem ser exploradas em outro momento na sala de aula.

Atividade 1: Durante uma partida do jogo “subindo e escorregando”, um jogador efetuou o
                       seguinte registro em sua tabela:

Jogador	Dado verde	Dado branco	Registro
A			4 + 4 – 6 = 2

Ä  Que número saiu em cada um dos dados? (verde e branco).

Ä  Em que casa este jogador estava?

Ä  O jogador voltou ou avançou em relação à casa em que estava?

Atividade 2: Durante uma partida você lançou os dados e efetuou a anotação.

Jogador	Dado verde	Dado branco	Registro
A	5	4

Ä  Você foi parar acima ou abaixo da casa em que você estava?

Ä  Quantas casas acima ou abaixo?

Atividade 3: Mostre que você agora já é fera no jogo!

Ä  O jogo mal começou e Liliana mostrou que está com sorte. Foi o mais alto que se pode ir na primeira rodada. Em que casa Liliana foi parar?

Ä  É possível alguém, na primeira rodada, já vencer o jogo? E na segunda? Explique como você pode fazer essa afirmação.

Ä  Na primeira rodada, é possível alguém cair fora da brincadeira? E na segunda? Explique como você pode fazer essa afirmação.

Ä  Ao fim da primeira rodada, a diferença máxima possível entre dois jogadores é de quantas casas?

Jogo: dominó do tangram

Número de participantes: até quatro jogadores.

Objetivos	. Relacionar frações às figuras do Tangram; . Utilizar conceito de equivalência de frações para comparar, simplificar,   adicionar e subtrair frações; . Identificar as figuras planas (quadrado, triângulo e paralelogramo) a   partir da construção do Tangram.
Material	. 28 peças do dominó; . Lápis e borracha.

Regras do jogo:

1. Dividir a turma em grupos com quatro alunos formando duas duplas (sugere-se que um aluno
    de cada dupla tenha mais habilidade em manipular frações);

2. Distribuir 7 peças para cada dupla e separar as restantes para futuras “compras”;

3. Tirar “par ou ímpar” e a dupla ganhadora inicia o jogo colocando uma peça (aleatoriamente) na
    mesa;

4. A outra dupla deve encontrar em uma de suas peças, aquela cuja quantidade corresponda a
    uma das metades indicada na peça que se encontra na mesa. Encaixando uma representação
    fracionária a uma representação geométrica ou, vice-versa;

5.  Toda vez que a dupla não tiver uma peça que satisfaça às condições da etapa 4, terá que
   “comprar” peças até conseguir uma, que se encaixe nas peças da mesa, ou até que se esgotem
    todas as peças;

6. Quando não existirem mais peças para serem “compradas”, a dupla passará a sua vez;

7. Será vencedora a dupla que terminar suas peças primeiro ou ficar com menor número de
    peças, quando não houver mais possibilidade de encaixes das peças restantes;

8. Cada jogador deve efetuar seu registro anotando como pensou a representação fracionária da
    forma geométrica ou  a representação geométrica da forma fracionária.

Explorando o jogo:

Professor, essas são atividades que podem ser exploradas em outro momento na sala de aula.

Ä  Proponha aos alunos que identifiquem a fração que representa a parte de um todo do tangram ou de outras figuras descrevendo uma classe de equivalência;

 

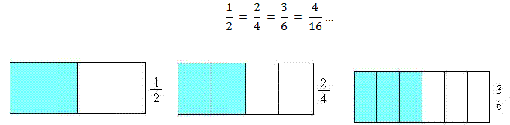
Ä  Solicitar que os alunos, a partir dessas representações, efetuem adições e subtrações entre frações de um mesmo conjunto de frações equivalentes sem o uso do cálculo do MMC (Mínimo múltiplo comum). Por exemplo:

 

Ä  Efetuar o cálculo de frações com denominadores diferentes explorando o conceito de frações equivalentes.

Ä  Explorar atividades que indiquem a mesma representação fracionária de grandezas diferentes. Por exemplo:

Esse     é a mesma coisa?

Jogo: corrida de obstáculos

Número de participantes: de dois a quatro alunos

Objetivos	.Explorar cálculos com expressões algébricas; .Possibilitar que os alunos percebam e expressem propriedades     matemáticas relativas ao cálculo algébrico, especialmente no que se  refere ao cálculo de valor numérico.
Material	. Tabuleiro do jogo; . Um dado; . Peões; . 18 cartas com números positivos, sendo três cartas de cada um dos seguintes valores: +1, +2, +3, +4, +5, +6 e, 18 cartas de números negativos, sendo 3 cartas de cada um dos valores: -1,-2, -3, -4, -5, -6 e 4 cartas zero. . Papel e lápis.

Regras do jogo:

1. As cartas são embaralhadas e colocadas nos respectivos lugares no tabuleiro formando três
    montes, viradas para baixo;

2. Os jogadores posicionam seus peões sobre o tabuleiro no ponto de partida;

3. Cada jogador, na sua vez, lança o dado e avança o número de casas igual ao número obtido no dado e retira uma carta de um dos montes à sua escolha;

4. O valor da carta deve substituir a variável da expressão algébrica da casa onde seu peão está.

5. Cada jogador efetua e registra seus cálculos e, o resultado obtido indica o valor e
     o sentido do movimento; se for positivo, o peão do jogador avança o número correspondente
     de casas; se for negativo, recua o correspondente ao número de casas; se for zero, o peão
     não se desloca e o jogador passa a vez ao adversário;

6. Se o peão cair numa casa que contém uma instrução, o jogador deverá executá-la nessa
     mesma jogada.

7. A partir da primeira rodada não se usa mais o dado: cada jogador movimenta seu peão
     escolhendo uma carta executando a instrução da casa onde se encontra o peão segundo as
     regras acima;

8. Sempre que o jogador escolher um número que anule o denominador da expressão, deverá voltar à casa de partida;

9. O vencedor é o jogador que completar em primeiro lugar duas voltas no tabuleiro;

10. Caso um dos três montes de carta esgote-se antes do final do jogo, então as respectivas
   cartas devem ser embaralhadas e recolocadas no tabuleiro;

11. Cada jogador deve efetuar seu registro anotando a expressão da casa em que o peão parou
      e os cálculos em cada jogada.

Explorando o jogo:

Ä  O jogo possibilitará que várias outras relações sejam exploradas, como por exemplo, o da regularidade do resultado na casa.

Ä  É possível saber o valor da expressão quando b for igual a 100, com base na sua investigação?

Ä  Investigações semelhantes permitirão que os alunos concluam que  é igual a n.

Ä  O jogo permite ainda a introdução do conceito de função, sendo que cada casa representa a expressão algébrica de uma função e as cartas do conjunto.

MEDIAÇÃO DE JOGOS NA SALA DE AULA PARA FAVORECER
APRENDIZAGEM MATEMÁTICA

Pesquisas demonstram que durante o jogo espontâneo, várias habilidades matemáticas são mobilizadas pelo aluno, entretanto, as mesmas quando necessárias na resolução de atividades em sala de aula,  bnão são mobilizadas. Uma das hipóteses para esta dissociação esta no fato de não relacionarem o jogo espontâneo com o estudar, visto que, estudar requer atenção, compromisso e dedicação, o que aparentemente não é exigido no jogo espontâneo.

Para utilizar o jogo em sala de aula, é preciso perceber que, além do conhecimento espontâneo, também está imbricado o conhecimento cientifico.

Precisamos assumir que a mediação da aprendizagem pelo jogo é complexa e incerta, quando se busca garantir a assimilação de determinados processos descritos, principalmente, porque a criança é capaz de dar respostas nem sempre desejadas ou esperadas pelo professor, e nem tampouco pela escola. Desta forma, o professor, ao planejar o jogo para o uso sala de aula, deverá pensar em ações de mediação durante as interações entre os alunos.

Para o educador matemático Cristiano Muniz (2010), existem seis categorias possíveis de conceber a mediação do jogo em sala de aula, que tem por objetivo a realização de determinadas aprendizagens a partir da estrutura lúdica.

ü    Transferência do jogo espontâneo para uma situação escolar;

ü    Realização de um debate sobre o jogo espontâneo;

ü    Transferência do jogo espontâneo a uma situação escolar, onde o aluno deve responder às questões colocadas pelo professor;

ü    A transferência do jogo espontâneo à sala de aula ou outro espaço escolar, onde o professor é um dos jogadores;

ü    O professor adapta o jogo que inicialmente era espontâneo e presente na cultura lúdica;

ü    O professor cria e oferece um jogo às crianças que é totalmente novo em função de um ou mais objetivos educativos.

A partir da mediação o professor poderá coletar informações do processo de aprendizagem do aluno, por meio do pensamento escrito, da oralidade e dos registros escritos.

Na tabela a seguir, apresentamos orientações do uso de jogo em sala de aula, com o intuito de revelar e/ou consolidar o conhecimento matemático.

ORGANIZAÇÃO DIDÁTICA
ENCAMINHAMENTOS METODOLÓGICOS	SALA DE AULA
	INICIANDO O JOGO	DURANTE O JOGO		DEPOIS DO JOGO
Planejamento	Ler as regras		Acompanhar		Socialização e reflexão
Conversas	Formas de início		Atenção às dificuldades		Formas de registros
Conhecimento do jogo	Registros escritos		Boas questões		Relatórios escritos